A SAMPLE OF OUR METHOD
Note from Dr. Monk: We still regularly utilize each of the 9 steps below in our daily practice. However, I have recently developed an even more effective technique called Functional Bio-Analysis (FBA), the subject of my book, Hope for Health, which was released in the spring of 2011. I have found FBA to far surpass all other natural manual muscle testing methods as practiced today.
Every part of the body is to some degree influenced by all the other parts. This idea can be clearly demonstrated when attempting to correct a chronic illness. In most cases, by the time the patient reaches our office, they have been dealing with one or more chronic issues for many years. In order for healing to take place, chronic illnesses require that all of the body’s systems (structural, chemical, emotional) be addressed, often at the same time – a whole person approach. This means that the primary goal is to use as many stress-reducing tools as possible on each visit with the patient. However, in difficult cases, the order in which these techniques are used can be just as important as the techniques themselves.
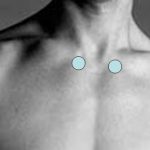
1. Brain Balancing – Under prolonged stress (structural, chemical or emotional) an interesting neurological phenomenon occurs; the communication between the brain and the rest of the body becomes distorted. In applied kinesiology the term is called “switching”. It is common for the person who is switched, to feel confused or “foggy-brained”. They often turn left when meaning to turn right, or they may stumble over their words when trying to describe a situation. There are some easy and quick exercises (Cross Crawls) and reflex points to correct this situation. A main set of points is located just below the collar bones called K27 (for their location on the kidney acupuncture merdians). Cross Crawls are a very simple exercise with often profound effects.
2. Check for subclinical infections – A subclinical infection cannot be found on a blood test. Discovery often require less orthodox techniques. Almost every person has some form of subclinical infection. Elimination of these organisms is critical. For more information on the detrimental effects of microorganisms see my article on Candida.
3. Check for food allergies – It has been estimated that up to 80% of headaches are caused by some form of food allergy. When the immune system is suppressed from poor lifestyle choices, food allergies often result. For more information see: Allergies.
4. Check for metal body burdens – Heavy metal poisoning is becoming more of a problem than most realize. Symptoms can include everything from loss of memory to bipolar disorder. The removal of heavy metals from the body can be multifaceted. It is not unusual for symptoms to change or even temporarily get worse. The patient should be advised that removing heavy metals is a process that requires consistent treatment over the course of many months.
5. Nutritional corrections – Without proper rebalancing of deficient nutrients the body simply will not be able to function at a high level. Proper nutrition through diet and supplementation is critical. For more information see: Nutritional Supplementation: A Life or Death Decision?
6. Desensitization (Neuro-Immune Treatment – N.I.T) – This is the process where I use acupressure points, neurolymphatic reflex areas, IRT, and in some cases laser light to lower the body’s response to a food (allergy) or an organism (infection). This step is done on all chronically ill patients. If not performed 30% or more will not fully recover.
7. Structural corrections – Correcting structure even in cases where it seems unnecessary such as with allergies or digestive problems is often times essential. Nerves and muscles all have direct relationships with organs. Fixing unbalanced structure takes tremendous stress off the body as a whole making recovery quicker and more likely.
8. Emotional corrections
9. Lifestyle modifications – These are critical in the initial recovery and for continued health once treatment has stopped.
The Up’s and Down’s of Chronic Illness
Correcting chronic illness is a process. Sometimes fantastic results are seen in the first few weeks. Other times the changes are slow and steady. It is also likely that there will be peaks and valleys as the patient learns to cope with their new lifestyle. For instance, if food allergies are part of the patient’s condition, then an avoidance of the food becomes necessary for a period of time – and on rare occasions, indefinitely. If they eat the food in the future, they may begin to experience detrimental symptoms of some kind. This is a gentle reminder that this particular food is detrimental. Patients should see this response as a blessing and heed the warning of their body.
Inertia is the law that says that an object in motion tends to stay in motion unless acted upon by an opposing force. Likewise, an object at rest tends to stay at rest unless acted upon by an opposing force. The same applies to the chronically ill person. Remember that a chronic illness by definition has been a part of a patient’s life for a long time. Poor lifestyle choices made over a lifetime have only permitted the body to move in one direction; an unhealthy direction. The result is both a metabolic and physiologic compensation. Symptoms such as high blood pressure, fatigue, joint pain, weight gain, anxiety, confusion and so on, are all examples. Continual compensation for bad choices without rest or replenishment is a significant stress that will eventually lead to a known condition or disease. The only way to restore health is to act in the body’s best interest by applying a force in the opposite direction. This process will require work. And work, as we all know, is often unpleasant.
There will be signs that the body is resisting change. From headaches to fatigue, any number of symptoms are possible. This makes sense given that the habits of the body have been firmly ingrained through years of bad choices. Some call these episodes a, “healing crisis”. The good news is that with my treatment programs most people experience very few if any significant side effects. For those who do, the highs are often much higher than the lows are low.
Glossary Of Terms
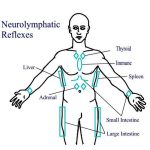
- Neurolymphatic Reflex Stimulation – These reflexes are located throughout the trunk and extremities. They relate to both a particular muscle and a particular organ (i.e. thigh muscles relate to the small intestine). Stimulating these reflexes with gentle circular pressure often produces a dramatic increase in the function of the related muscle and organ.
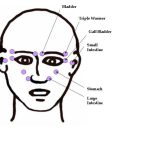
- Neurovascular Reflex Stimulation – Like neurolymphatic reflexes that have both a muscle and an organ related to them, neurovascular reflexes have similar relationships but are located on the head. Light sustained pressure is all that is required to stimulate these reflexes and produce a therapeutic effect.
- Beginning and Ending points – These are points located on the face. They are either the beginning or the ending of certain acupuncture meridians. Tapping these points can be extremely helpful to the patient who suffers from allergies or an infection.
- Injury Recall Technique (IRT) – When a tissue is injured, the body places a high priority on its healing. Also, all sorts of chemical and neurological processes begin. During the healing process the tissue will be in a state of reduced function and will likely be painful or sensitive to touch. That is because the sensory nerves located around and within the tissue are on high alert. This state reminds the rest of the body that this area is under repair. The nerves will maintain their state of heightened sensitivity until complete healing has occurred. Sometimes, for whatever reason, this does not take place, and so tissue function is reduced and the nerves remain highly sensitive. When present, a deeper neurological therapy is required in order for proper function to be restored. The procedure is very simple, but often produces a surprisingly strong therapeutic response. Two steps are required. 1. The doctor stimulates the previously injured area – usually with gentle pinching. 2. The doctor then immediately applies gentle downward pressure on a bone in the foot called the talus. That’s it! The neurological explanation for the effectiveness of this treatment is somewhat complicated and has to do with all of the sensory nerves located throughout the foot. The messages from these nerves are given a high priority in the brain because they are responsible for keeping us upright and oriented when we stand on our feet. Somehow, stimulating a previously injured area and then immediately stimulating the sensory receptors in the foot, produces a reduction in nerve sensitivity and an increase in function of the previously injured tissue. One patient had a return of normal vision as a result IRT. She was struck in the head with a discus many years prior, and gradually her eyesight worsened. After performing this simple procedure on the scarred area where the impact occurred her vision returned to normal within fifteen minutes. This response is in no way typical but it does demonstrate that subtle corrections in the nervous system can have dramatic results.
- Laser Therapy – Cold Lasers, as they are called, are rapidly increasing in interest for natural healing professionals. They are now known to have many health benefits including: pain reduction, increasing endorphins, Increased ATP production (energy), increased cell metabolism, collagen synthesis (tissue repair), local effects on the immune system, and many other measured effects. Personally I used a small laser on some specific acupuncture points to aid in the recovery of allergies and infections. I would not be surprised if lasers are a standard of care in health care offices in the next few years.